로지스틱 회귀(Logistic Regression)는 데이터가 어떤 범주에 속할 확률을 0에서 1 사이의 값으로 예측한 후, 그 확률에 따라서 더 가능성이 높은 범주에 속하는 것으로 분류해주는 지도학습 알고리즘입니다. 예를들면 스팸 메일 분류같은 것이 있습니다. 스팸 분류기는 어떤 메일을 받았을 때 스팸일 확률이 50% 이상이면 스팸으로 아니면 스팸이 아닌 것으로 분류하여 줍니다. 이렇게 2개의 범주로 나누는 것을 2진 분류(Binary classification)이라고 하고 3개 이상으로 나누는 것을 다중분류(Multi-class classification)이라고 합니다.
step 1. Logistic Function (Sigmoid Function)
Logistic regression을 진행하기 위해서는 출력 값을 0과 1의 값으로 맞춰주어야 합니다. 이를 위해서 우리는 Logistic Function 을 사용합니다. Logistic Function은 다음과 같습니다.
$$\sigma(z) = \frac{1}{1 + e^{-z}}$$
Logistic regression을 진행할 때 입력 데이터를 $x$, 실제 class 값을 $y$, 예측된 출력 값을 $\hat{y}$라고 하면 $x$는 두가지 변환을 거쳐서 $\hat{y}$가 됩니다.
$$z = wx + b$$
$$\hat{y} = \sigma(z)$$
우리의 목표는 $\hat{y}$이 실제 $y$와 가장 가깝게 되도록 하는 $w$와 $b$를 찾는 것 입니다.
그럼 Logistic function을 코드를 통해서 알아보도록 하겠습니다.
import sympy
import numpy
from matplotlib import pyplot
%matplotlib inline
z = sympy.Symbol('z', real=True)
logistic = 1/(1+ sympy.exp(-z))
print(logistic)
sympy.plotting.plot(logistic);
위 그래프를 보면 $z=0$ 일 때 출력 값이 0.5가 됩니다. 그리고 양수 일 때는 1에 음수일 때는 0에 가까워지게 됩니다. 이렇게 $z$값을 0과 1 사이로 표현할 수 있게 되었습니다.
이제 데이터를 직접 만들어서 진행해봅니다. numpy에 random함수를 통해 조금의 noise를 섞어서 데이터를 생성했습니다.
# synthetic data
x_data = numpy.linspace(-5, 5, 100)
w = 2
b = 1
numpy.random.seed(0)
z_data = w * x_data + b + numpy.random.normal(size=len(x_data))
y_data = 1 / (1+ numpy.exp(-z_data))
pyplot.scatter(x_data, y_data, alpha=0.4);
실제 class 값을 정해줍니다. Numpy 패키지 안의 where 함수로 0.5보다 큰 값을 1, 작은 값을 0으로 class 값을 부여해줍니다.
y_data = numpy.where(y_data >= 0.5, 1, 0)
pyplot.scatter(x_data, y_data, alpha=0.4);
Step 2. Logistic Loss Function
$\hat{y}$가 실제 $y$와 가장 가깝게 되도록 하는 $w$와 $b$를 찾으려면 먼저 cost function을 정의해야 합니다.
Linear regression 문제를 해결할 때는 Mean Square Error를 사용했습니다.
하지만 logistic regression에 적용하면 문제가 생깁니다.
기존의 linear regression에서의 Mean Square Error 에서는 $\frac{1}{n} \sum_{i=1}^n (y_i - (wx_i + b))^2$ 의 형태를 이루고 있어서 볼록(convex)한 형태를 이루고 있었습니다.
그런데 logistic function을 포함한 logistic regression에서는 $\frac{1}{n} \sum_{i=1}^n (y_i - \sigma(wx_i + b))^2$ 가 $\sigma$인 logistic function 때문에 더이상 볼록(convex)한 형태가 아닙니다. 예시를 통해서 왜 볼록한 상태가 아닌지 알아보겠습니다.
간단한 예시를 위해 $w = 1, b=0$일 때 3개의 데이터를 통해서 알아보겠습니다.
$(x, y) : (-1, 2), (-20, -1), (-5, 5)$ 일 때 cost function을 그래프로 나타내면 다음과 같습니다.
badloss = (2 - 1/(1+ sympy.exp(-z)))**2 + \
(-1 - 1/(1+ sympy.exp(-20*z)))**2 + \
(5 - 1/(1+ sympy.exp(-5*z)))**2
print(badloss)
sympy.plotting.plot(badloss, xlim=(-1,1));
만약 Gradient Descent 방식으로 위 Cost Function의 최솟값을 구하게 되면 중간에 기울기가 0인 지점에서 멈추게 될 것입니다.
그래서 Mean Square Error(MSE)말고 다른 방법을 찾기 위해 Cost Function의 의미를 다시 한 번 생각해 보겠습니다.
만약 어떤 값을 예측할 때 많이 틀렸다면, 예측하는데 쓰인 변수들을 많이 바꾸어야 합니다. 그에 비해 조금 틀렸다면, 이미 잘 예측하고 있기 때문에 변수들을 조금 바꾸어야 합니다. 많이 바꾸고, 조금 바꾸는 것은 기울기의 크기가 정합니다. 이러한 원리를 사용해서 linear regression에서는 Square Error를 쓰는 것입니다.
이 원리를 logistic regression에도 적용해 보겠습니다.
$z = wx + b$ 일 때 cost function $L$을 b에 대해서 미분을 해보겠습니다. Chain Rule을 사용하면 다음과 같게 됩니다.
$$\frac{\partial{L}}{\partial{b}} = \frac{\partial{L}}{\partial{\sigma(z)}} \frac{\partial{\sigma(z)}}{\partial{z}}\frac{\partial{z}}{\partial{b}}$$
이 때, $\frac{\partial{z}}{\partial{b}}$는 1이 돼서 사라집니다.
이제 $\frac{\partial{\sigma(z)}}{\partial{z}}$에 대해서 알아봅니다.
lprime = logistic.diff(z)
print(lprime)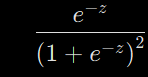
위에서 나온 $\sigma'(z)$를 정리하면 $\frac{\partial{\sigma(z)}}{\partial{z}} = \frac{e^{-z}}{(1+e^{-z})^2} = \frac{1}{1+e^{-z}} \times \frac{e^{-z}}{1+e^{-z}} = \sigma(z)\times \frac{e^{-z}}{1+e^{-z}} $ 가 되고, 여기서 $\frac{e^{-z}}{1+e^{-z}} $를 다시 정리하면 다음과 같습니다.
$$\frac{e^{-z}}{1+e^{-z}} = \frac{1 + e^{-z} -1}{1 + e^{-z}} = 1 - \frac{1}{1+e^{-z}} = 1-\sigma(z)$$
결론적으로, $\sigma'(z)$ 는 $\sigma(z) ( 1 - \sigma(z))$ 가 됩니다.
다시한번 위 식을 정리해보면 다음과 같습니다.
$$\frac{\partial{L}}{\partial{b}} = \frac{\partial{L}}{\partial{\sigma(z)}} \frac{\partial{\sigma(z)}}{\partial{z}} = \frac{\partial{L}}{\partial{\sigma(z)}} \sigma(z) (1-\sigma(z))$$
여기서 $\frac{\partial{L}}{\partial{b}}$의 값은 예측 값과 실제 값의 차이가 클수록 크고, 작을수록 작아야 되기 때문에 $\frac{\partial{L}}{\partial{b}} = (y - \sigma(z))$로 정의합니다. 다시 정리하면 다음과 같습니다.
$$\frac{\partial{L}}{\partial{\sigma(z)}} = \frac{(y-\sigma(z))}{\sigma(z)(1-\sigma(z))}$$
이제 위 식을 $L$에 대해서 코드를 통해서 정리해봅니다. 코드를 간단히 하기 위해서 $\sigma(z) = a$라고 치환합니다.
a, y = sympy.symbols('a y', real=True)
dLda = (y-a)/a/(1-a)
print(dLda)
L = sympy.integrate(dLda, a)
print(L)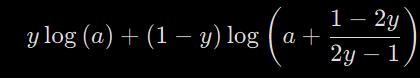
sympy.simplify(L)
여기서 $a = \sigma(z)$이기 때문에 $ a < 1 $이 됩니다. 그래서 $\log$ 안의 값이 음수가 되면 안되기 때문에 식을 변환해 줍니다.
L = -y*sympy.log(a) + (y-1)*sympy.log(1-a)
print(L)
우리가 구한 cost function $L$은
$$L = -y \log(a) + (y-1)\log(1-a)$$이 됩니다.
이제 실제로 차이가 클 때 $L$값이 커지는지 알아봅니다.
먼저 만약 $y=1$이라면 $L = -\log(a)$만 남게 됩니다. 그래프로 표현하면 다음과 같습니다.
sympy.plotting.plot(-sympy.log(a), xlim=(0,1));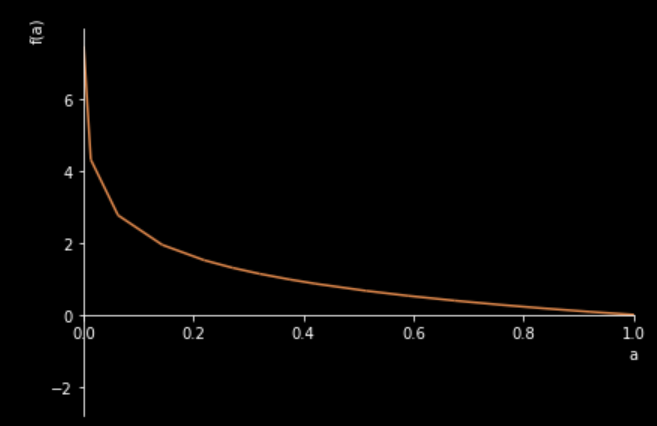
이제 $y=0$이라면 $L = \log(1-a)$ 만 남게 됩니다. 이를 또한 그래프로 표현하면 다음과 같습니다.
sympy.plotting.plot(-sympy.log(1-a), xlim=(0,1));
이번에도 예측값이 실제 값이랑 가까워지면 cost function값이 작아지고 멀어지면 커지게 됨을 알 수 있습니다.
Step 3. Find the parameters using autograd function
이제 logistic regression의 전체적인 과정을 코드를 통해서 알아보도록 하겠습니다.
print(logistic)
w, b, x, y = sympy.symbols('w b x y')
logistic = 1/(1+ sympy.exp(-w*x-b)) # redefined with the composition
Loss = -y*sympy.log(logistic) - (1-y)*sympy.log(1-logistic)
print(Loss)
지금까지 diff 를 통해서 기울기를 구했습니다. 그런데 식이 복잡해질수록 속도가 느려지기 때문에 autograd를 통해서 구해보겠습니다.
# import the autograd-wrapped version of numpy
from autograd import numpy
# import the gradient calculator
from autograd import grad
# note: the namespace numpy is the autograd wrapper to NumPy
def logistic(z):
'''The logistic function'''
return 1 / (1 + numpy.exp(-z))
def logistic_model(params, x):
'''A prediction model based on the logistic function composed with wx+b
Arguments:
params: array(w,b) of model parameters
x : array of x data'''
w = params[0]
b = params[1]
z = w * x + b
y = logistic(z)
return y
def log_loss(params, model, x, y):
'''The logistic loss function
Arguments:
params: array(w,b) of model parameters
model: the Python function for the logistic model
x, y: arrays of input data to the model'''
y_pred = model(params, x)
return -numpy.mean(y * numpy.log(y_pred) + (1-y) * numpy.log(1 - y_pred))
# get a function to compute the gradient of the logistic loss
gradient = grad(log_loss)이 떄 grad 함수는 변수 개수만큼 output을 만들게 됩니다. 우리는 $w, b$ 2개의 변수가 있습니다. 먼저 예시로 랜덤으로 초기화한 변수를 넣어서 기울기값을 구해보겠습니다.
numpy.random.seed(0)
params = numpy.random.rand(2)
print(params)
gradient(params, logistic_model, x_data, y_data)
이렇게 2개의 변수에 대해서 각각 기울기 값을 반환해줍니다.
이번에 gradient descent 를 진행할 때는 새로운 조건을 추가해서 진행합니다. 우리가 정한 반복 수 외의 기울기 값이 0에 가까워지면 더이상 반복을 하지 않는 조건을 추가합니다. 0에 가까운 값을 설정한 뒤 그것보다 작아지면, while 문이 멈추도록 설정하여서 gradient descent 를 진행합니다.
max_iter = 5000
i = 0
descent = numpy.ones(len(params))
while numpy.linalg.norm(descent) > 0.001 and i < max_iter:
descent = gradient(params, logistic_model, x_data, y_data)
params = params - descent * 0.01
i += 1
print('Optimized value of w is {} vs. true value: 2'.format(params[0]))
print('Optimized value of b is {} vs. true value: 1'.format(params[1]))
print('Exited after {} iterations'.format(i))
pyplot.scatter(x_data, y_data, alpha=0.4)
pyplot.plot(x_data, logistic_model(params, x_data), '-r');
파란색 곡선이 모델입니다.
이제 기준값을 정하고 그것보다 크면 1, 작으면 0으로 분류를 하면 됩니다.
이번에는 0.5로 설정해서 진행합니다.
def decision_boundary(y):
return 1 if y >= .5 else 0모든 점을 함수에 넣어야 하는데 하나씩 넣으면 반복문을 돌아야해서 오래걸리기 때문에 numpy의 vectorize 함수를 사용합니다.
decision_boundary = numpy.vectorize(decision_boundary)
def classify(predictions):
'''
Argument:
predictions, an array of values between 0 and 1
Returns:
classified, an array of 0 and 1 values'''
return decision_boundary(predictions).flatten()
pyplot.scatter(x_data, y_data, alpha=0.4,
label='true value')
pyplot.scatter(x_data, classify(logistic_model(params, x_data)), alpha=0.4,
label='prediciton')
pyplot.legend();
이로서 거의 모든 데이터를 정확하게 예측하였습니다.
Logistic Regression을 이용하면 2진분류 (Binary classification)뿐만아니라 다중분류(Multi-class classification)도 할 수 있습니다. 다중분류를 할 때는 분류하고 싶은 종류마다 모델을 만들고 각각 확률이 높은 모델의 결과를 사용하면 됩니다.
예를들어 사람, 고양이, 강아지를 구분하는 모델을 만들고 싶으면, 사람만을 구분하는 모델, 고양이만 분류하는 모델, 강아지만 분류하는 모델을 만들어줍니다. 그리고 각 모델을 병렬적으로 돌려서 확률이 가장 높은 모델의 분류를 따릅니다.
자세한 내용은 아래 링크를 확인해주세요.