[ML 머신러닝] K-Means Clustering K-평균 군집

목표 값(Target Variable)을 모르는 즉, 정답(Ground Truth, 기상학 용어로 '기상 실측 정보', 보통 '실제 값'이라고 번역 됨)을 모르는 상태로 학습을 하는 것을 비지도학습(Unspervised Learning)이라고 합니다. K-평균 군집 알고리즘(K-Means Clustering Algorithm)은 대표적인 비지도학습(Unspervised Learning) 알고리즘입니다.

 

Step 1. Introduction to K-Means Clustering

K-평균 군집(K-Means Clustering)은 분류가 되어있지 않은 데이터를 미리 정해놓은 개수 K개의 클러스터로 주어진 데이터를 묶어내는 방법론입니다. 주어진 데이터들을 클러스터 중 하나로 배정하는 방법으로 학습이 진행됩니다. 이를 반복하다보면 결국 가까운 데이터들끼리 같은 클러스터에 할당됩니다. 이미지로 나타내면 다음과 같습니다.

Step 2. K-Means Clustering Intuition

K-평균 군집(K-Means Clustering)은 레이블이 지정되지 않은 데이터를 중심부(Centroid)를 기반으로 군집화(Clustering)합니다. 이 때 중심부는 각 클러스터(Cluster)의 중심을 의미합니다. K-Means Clustering은 다음 2가지 Step을 반복적으로 수행합니다.

1. Data Assignment Step : 각 중심부(Centroid)는 하나의 클러스터(Cluster)를 의미합니다. 모든 데이터들은 각자 자신과 가장 가까운 중심부(Centroid)에 해당하는 클러스터(Cluster)에 속하게 됩니다.
2. Centroid Update Step : 모든 데이터(Data)가 각각의 클러스터(Cluster)에 배정되었다면, 이제 클러스터(Custer)에 속해 있는 데이터(Data)들의 평균 값으로 중심부(Centroid)가 다시 갱신(Update)됩니다.

더 이상 데이터들의 클러스터가 변하지 않을 때까지 이 두 가지 과정을 반복적으로 수행하게 됩니다. 이 알고리즘은 반드시 수렴하게 되어있지만, 초기화 하는 방식에 따라서 local optimum으로 수렴하게 될 수도 있습니다.

이 과정을 그림으로 나타내면 다음과 같습니다.

△가 중심부(Centroid)이고, ○가 데이터로 2개의 군집을 형성하는 방법 

 Step 3. Choosing The Value of K

K-평균 알고리즘(K-Means Algorithm)은 미리 정해놓은 K에 값에 따라서 작동하게 됩니다. 그래서 가장 좋은 K의 값을 찾기 위해 여러가지 K값으로 알고리즘을 수행해 보고 비교해 보아야 합니다.

가장 좋은 K값을 찾는데 여러가지 방법이 있지만, 가장 대표적 방법인 Elbow Method를 사용해봅니다.

Step 4. The Elbow Method

The Elbow Method는 가장 좋은 K값을 찾는데 사용하는 방법입니다. 여러가지 K에 대해서 모두 실험을 해보고 해당 비용함수(Cost Function)를 그래프로 표현한 뒤 최적의 K값을 찾습니다.

K가 커질수록 비용함수(Cost function)가 줄어듭니다. 그러나 무작정 K의 개수를 키운다면 그것은 군집화(Clustering)을 하는 의미가 없어집니다. 그래서 비용함수(Cost function)가 가장 가파르게 줄어드는 마지막 지점의 K를 선택합니다. 이 방법을 Elbow Method라고 부릅니다. (Elbow Method는 따로 번역하지 않고 영어표현 그데로 사용하는 것같습니다. 직역하자면 팔꿈치 방법인데, 구부러진 모양이 팔꿈치같아서 그런 이름을 붙인거 같습니다.)

Step 5. Practice

먼저 실습용 데이터 셋을 가져옵니다. 데이터는 분꽃 분류 데이터를 이용합니다.

from urllib.request import urlretrieve
URL = 'https://gist.githubusercontent.com/netj/8836201/raw/6f9306ad21398ea43cba4f7d537619d0e07d5ae3/iris.csv'
urlretrieve(URL, 'Iris.csv')

필요한 모듈을 불러오고 dataset에 데이터를 받아줍니다.

#importing the libraries
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

#importing the Iris dataset with pandas
dataset = pd.read_csv('/content/Iris.csv')
x = dataset.iloc[:, [0, 1, 2, 3]].values

받아온 데이터가 잘 들어왔는지 확인해줍니다.

dataset.info()
dataset[0:10]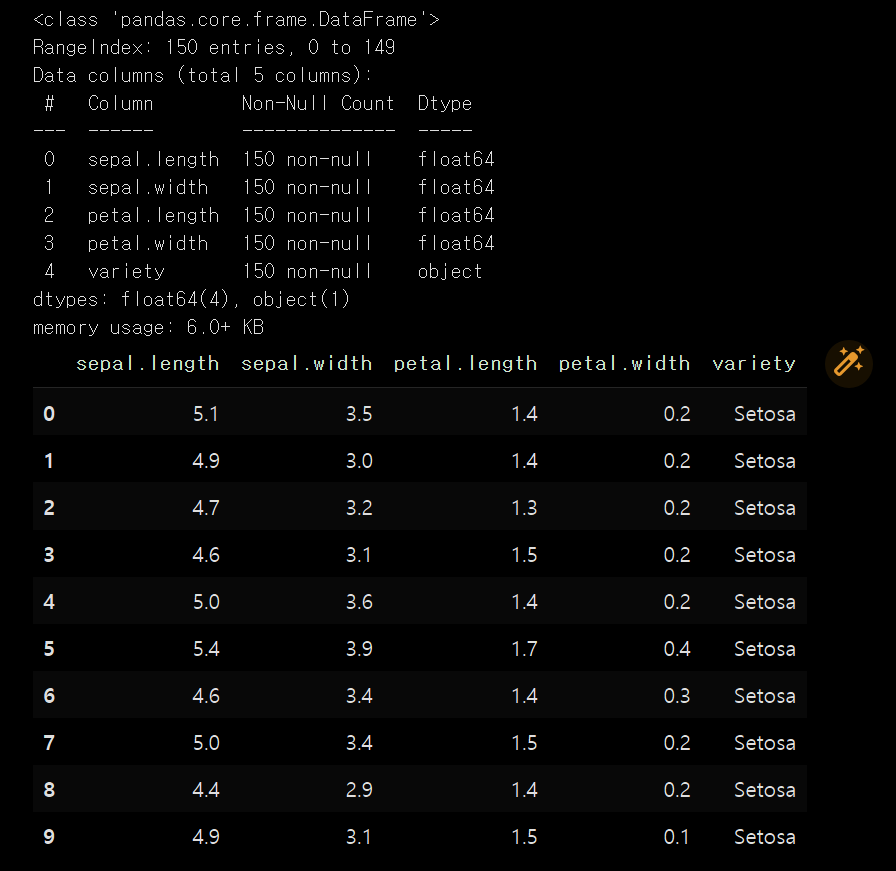

꽃받침과 꽃잎의 길이 넓이 데이터와 분꽃 종류가 데이터로 들어왔습니다.

이제 scikit-learn 속의 Kmeans 패키지를 이용해서 진행해봅니다.

K개수를 1부터 10까지 진행해보면서 목적함수(Cost function)인 inertia를 측정해보겠습니다.

#Finding the optimum number of clusters for k-means classification
from sklearn.cluster import KMeans
wcss = []

for i in range(1, 11):
    kmeans = KMeans(n_clusters = i, init = 'k-means++', max_iter = 300, n_init = 10, random_state = 0)
    kmeans.fit(x)
    wcss.append(kmeans.inertia_)

plt.plot(range(1, 11), wcss)
plt.title('The elbow method')
plt.xlabel('Number of clusters')
plt.ylabel('WCSS') #within cluster sum of squares
plt.show()

K를 3으로 설정한 후 K-Means를 수행해 보겠습니다.

kmeans = KMeans(n_clusters = 3, init = 'k-means++', max_iter = 300, n_init = 10, random_state = 0)
y_kmeans = kmeans.fit_predict(x)

#Visualising the clusters
plt.scatter(x[y_kmeans == 0, 0], x[y_kmeans == 0, 1], s = 100, c = 'purple', label = 'Iris-setosa')
plt.scatter(x[y_kmeans == 1, 0], x[y_kmeans == 1, 1], s = 100, c = 'orange', label = 'Iris-versicolour')
plt.scatter(x[y_kmeans == 2, 0], x[y_kmeans == 2, 1], s = 100, c = 'green', label = 'Iris-virginica')

#Plotting the centroids of the clusters
plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:,1], s = 100, c = 'red', label = 'Centroids')

plt.legend()

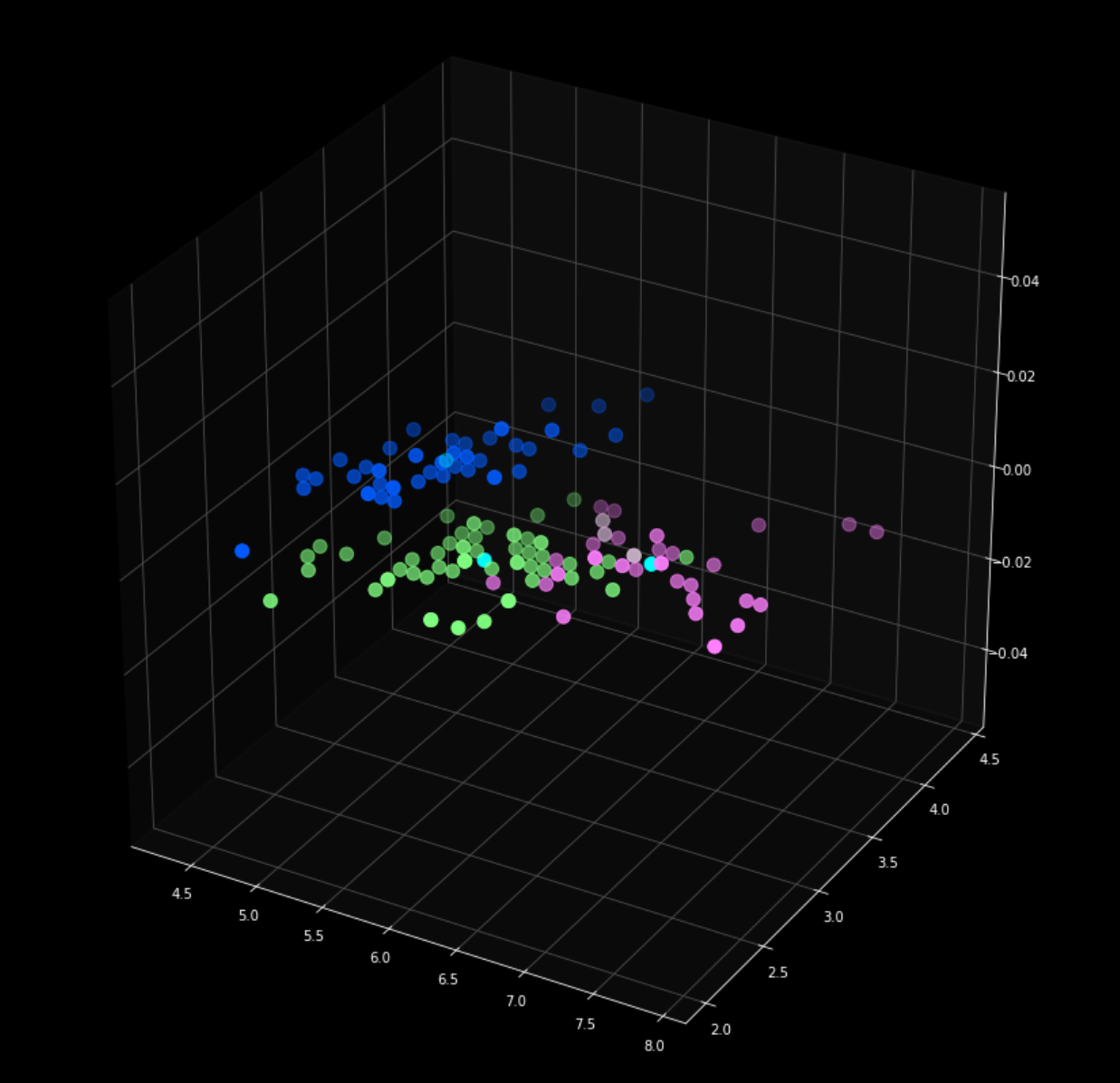
3차원 그래프로 표현해줍니다.

# 3d scatterplot using matplotlib

fig = plt.figure(figsize = (15,15))
ax = fig.add_subplot(111, projection='3d')
plt.scatter(x[y_kmeans == 0, 0], x[y_kmeans == 0, 1], s = 100, c = 'purple', label = 'Iris-setosa')
plt.scatter(x[y_kmeans == 1, 0], x[y_kmeans == 1, 1], s = 100, c = 'orange', label = 'Iris-versicolour')
plt.scatter(x[y_kmeans == 2, 0], x[y_kmeans == 2, 1], s = 100, c = 'green', label = 'Iris-virginica')

#Plotting the centroids of the clusters
plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:,1], s = 100, c = 'red', label = 'Centroids')
plt.show()